BZOJ1002 - Click Here
Description
轮状病毒有很多变种,所有轮状病毒的变种都是从一个轮状基产生的。一个N轮状基由圆环上N个不同的基原子和圆心处一个核原子构成的,2个原子之间的边表示这2个原子之间的信息通道。如下图所示
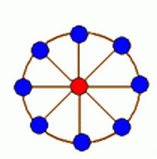
N轮状病毒的产生规律是在一个N轮状基中删去若干条边,使得各原子之间有唯一的信息通道,例如共有16个不同的3轮状病毒,如下图所示
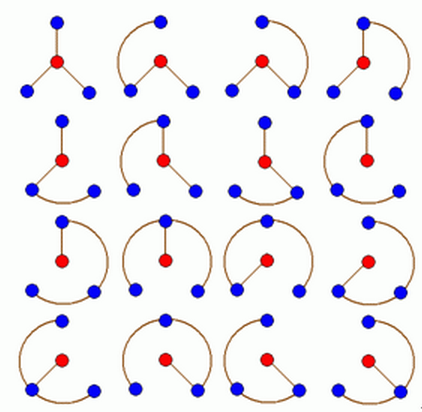
现给定n(N<=100),编程计算有多少个不同的n轮状病毒
Input
第一行有1个正整数n
Output
计算出的不同的n轮状病毒数输出
Solutions
考虑将病毒分成两部分,外围圆环和内部的核原子。
如果外围的划分确定,那么该外围划分对应的方案显然也是已知的。
因此现在的问题就是如何将外围圆环划分。
环问题不好处理,考虑将环转换成链。可以枚举一条通过节点1与节点n的信息通道,那么剩下部分显然是一条链。
而链的问题可以用DP解决。设$f(i)$为链长为$i$的划分方案,则有转移方程$f(i)=\sum_j f(i-j) \cdot j$
因此最终答案为$\sum_{i=2}^n \sum_{j=2}^n j \cdot f(n-j) = \sum_{i=2}^n j(j-1) \cdot f(n - j)$
时间复杂度为$O(kn^2)$,其中$k$为高精运算的时间复杂度。对于这题而言,压位后$k$大概是$5$左右。
CODE
CODE - Click Here