BZOJ1815 - Click Here
Description
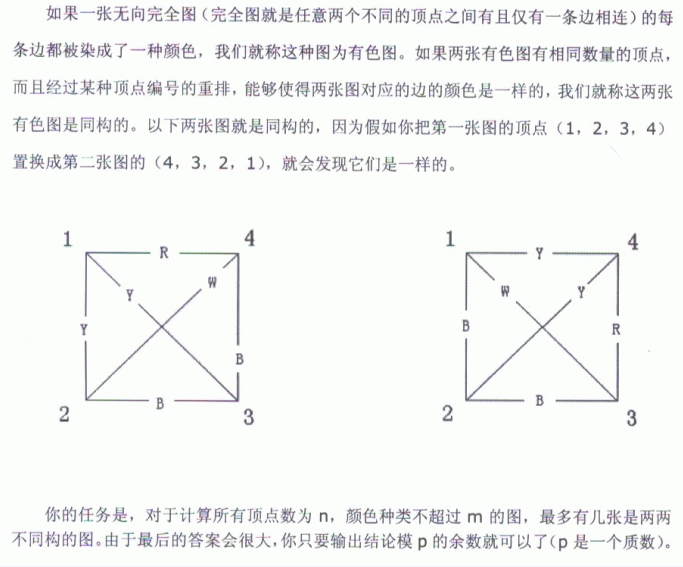
Input
输入三个整数N,M,P
1<=N<=53,1<=M<=1000,N< P<=10^ 9
Output
即总数模P后的余数
Solutions
并不会如何把点循环转换成边循环,因此在看题解前只会多个$n$的做法qwq
这题有个比较显然的结论,就是一个点置换对应着一个唯一的边置换。而且,边置换是成群的。
基于这个结论,容易得到一个$n!$级别的算法,即暴力枚举点置换,并计算出对应的边置换,然后套用Polya定理解决。但显然,这种做法是TLE的。
由于Polya定理需要的只是循环数,而不是置换循环分解的形式。因此可以得到另外一个结论,对于同一个共轭类的置换,其对应的边置换循环数是一样的。
同时,共轭类的大小也易得到,其大小为$\frac{n!}{\prod{c_i(p) \cdot i^{c_i(p)}}}$;其中$c_i(p)$表示循环长度为$i$的循环的个数。
基于上诉两点,可以得到一个较为优秀的做法:枚举共轭类,并暴力求出边置换的循环数。时间复杂度是$O(kn^3)$,其中$k$表示共轭类的数量。通过暴力枚举可得知,当$n=53$时,$k$是5e5级别的。
看起来已经足够了,但还是TLE!而时间的瓶颈就在于求出边置换的循环数。
考虑优化这个过程。
对于一条边而言,有两种情况:一种为循环内的边,一种为两个循环之间的边。
若为循环内的边,其产生的循环数相当于节点数为$L$的完全图的置换,其个数为$\frac{L}{2}$
若为两个循环间的边,其产生的循环数相当于集合大小分别为$L_1,L_2$的完全二分图的置换,其个数为$gcd(L_1,L_2)$
时间复杂度$O(kn^2)$
CODE
CODE - Click Here