BZOJ2159 - Click Here
Description
Crash 小朋友最近迷上了一款游戏——文明5(Civilization V)。在这个游戏中,玩家可以建立和发展自己的国家,通过外交和别的国家交流,或是通过战争征服别的国家。现在Crash 已经拥有了一个N 个城市的国家,这些城市之间通过道路相连。由于建设道路是有花费的,因此Crash 只修建了N-1 条道路连接这些城市,不过可以保证任意两个城市都有路径相通。在游戏中,Crash 需要选择一个城市作为他的国家的首都,选择首都需要考虑很多指标,有一个指标是这样的:
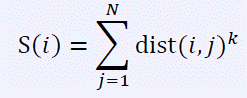
其中S(i)表示第i 个城市的指标值,dist(i, j)表示第i 个城市到第j 个城市需要经过的道路条数的最小值,k 为一个常数且为正整数。因此Crash 交给你一个简单的任务:给出城市之间的道路,对于每个城市,输出这个城市的指标值,由于指标值可能会很大,所以你只需要输出这个数mod 10007 的值。
Input
输入的第一行包括两个正整数N 和k。下面有N-1 行,每行两个正整数u、v (1 ≤ u, v ≤ N),表示第u 个城市和第v 个城市之间有道路相连。这些道路保证能符合题目的要求。
Output
输出共N 行,每行一个正整数,第i 行的正整数表示第i 个城市的指标值 mod 10007 的值。
Solutions
先讲个个人认为比较显然的做法。
定义$S_d(i)$表示与$i$距离为$d$的节点数,则题目实则是求$\sum_d S_d(i) \cdot d^k$
对于$i$的相邻节点$j$,有$\sum_d S_d(i) \cdot d^k = \sum_j \sum_d S_d(j) \cdot (d+1)^k$。
考虑对右式展开
令$f_k(i)=\sum_d S_d(i) \cdot d^k$,那么上式等价于$f_k(i) = \sum_j \sum_p \dbinom{k}{p} f_p(j)$
因此,如果能够维护相邻接点的$f_p(j)$,则能够在$k^2$时间复杂度内求出$f_k(i)$
考虑树形dp,对每个节点分别维护子树内的$f_p(i)$与非子树内$f_p(i)$,则能够利用上诉式子快速转移。
时间复杂度$O(nk^2)$
这题还有$O(nk)$做法,不过感觉没有上面做法自然,完全就是推公式…
定义$S_d(i)$表示与$i$距离为$d$的节点数,那么有$ans = \sum_d S_d(i) \cdot d^k$
考虑对右式展开
其中$S(n,m)$表示第二类斯特林数。
令$f_p(i) = \sum_d S_d(i) \dbinom{d}{p}$,则$ans = \sum_p S(k,p) \cdot p! \cdot f_p(i)$
那么现在的问题就是求$f_p(i)$。对于$i$的相邻节点$j$,有
同样的,考虑树形dp,分别维护子树与非子树的$f_p(i)$,并利用上式快速转移。
时间复杂度$O(nk)$
CODE
CODE($O(nk)$做法) - Click Here