COGS2897 - Click Here
Description
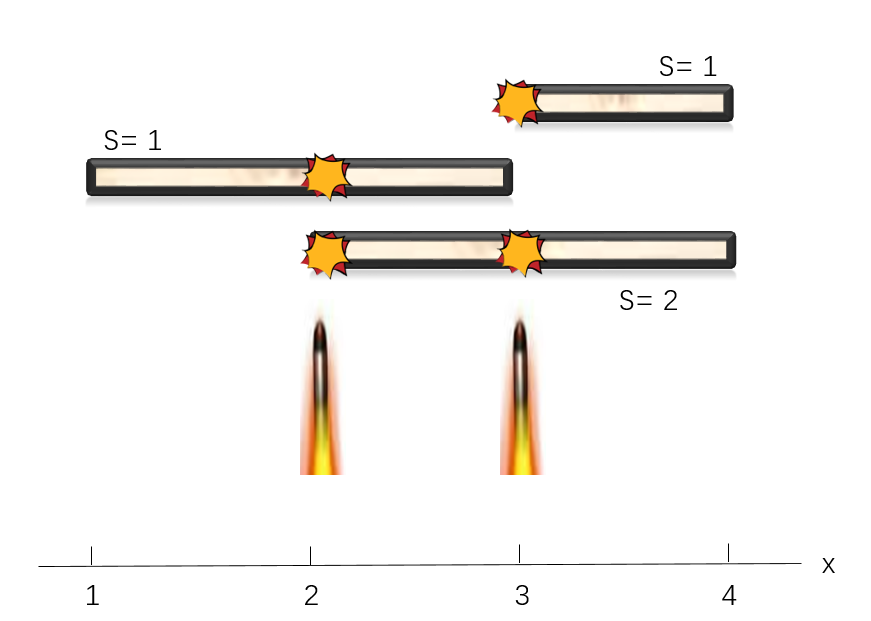
小C爱上了一款名字叫做《天天爱射击》的游戏,在这款游戏中可以用子弹将木板打碎。如图所示,这个游戏有一些平行于x轴的木板。现在有一些子弹,按顺序沿着y轴方向向这些木板射去。第i块木板被S_i个子弹击穿以后,就会碎掉消失。一个子弹可以贯穿其轨迹上的全部木板,特别的,如果一个子弹触碰到木板的边缘,也视为贯穿木板。
小C现在知道了游戏中n块木板位置,以及知道了m个子弹起始位置。现在问你每个子弹射出去以后,有多少木板会被击穿?
Input
第一行两个整数n和m,表示木板数量和子弹数量。其中1 <= n,m <= 200,000。
接下来n行,每行3个整数x_1,x_2,S,表示每块木板的左端点x坐标、右端点x坐标,以及贯穿多少次会碎掉。其中保证1 <= x_1 <= x_2 <=200,000 且1 <= S <=200,000。
接下来m行,每行一个整数x,表示每个子弹的x坐标。子弹按照发射顺序给出。其中保证1 <= x <= 200,000。
Output
m 行,每行一个整数。表示每颗子弹射出去后,有多少木板碎掉。
Solutions
似乎是THUPC2017的题。初次见到是在THUPC2018练习赛,那时候写了主席树做法,结果却一直WA,卡了一小时都没过。因此对这题怨念很大…
正着思考问题似乎很困难,我们考虑每个木板被哪个子弹破坏。
对于每个木板,能够二分答案求出是被哪个子弹破坏。同时注意到子弹间对木板的影响相互独立,因此能够整体二分解决。时间复杂度$O((n+m) \log m \log x)$。
该题还存在一个$\log$做法的。考虑到查询被哪个子弹破坏的过程,本质上是询问区间第$k$个($k$为贯穿数)射出的子弹。该问题为静态区间$k$大问题,可以直接主席树解决。时间复杂度$O(n \log x)$
CODE
CODE(主席树) - Click Here
CODE(整体二分) - Click Here