JZOJ3648 - Click Here
Description

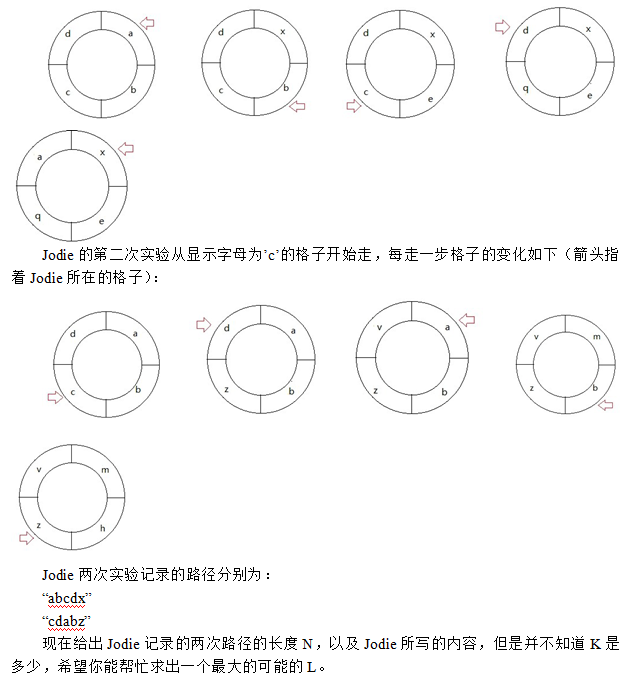
Input
第一行:包含一个整数N。
第二行:包含一个长度为N的字符串,字符串中只包含小写字母。
第三行:包含一个长度为N的字符串,字符串中只包含小写字母。
对于50% 的数据,1 <= N <= 600,000
对于100% 的数据,1 <= N <= 2,000,000
Output
输出答案只包含一个数字L,表示圆环最大可能有的格子数。
Solutions
先讲讲我的zz做法…
设两个字符串为$s_1,s_2$。$lcp_1(i)$表示以$i$开始的$s_1$后缀与$s_2$的最长公共前缀,$lcp_2(i)$表示以$i$开始的$s_2$后缀与$s_1$的最长公共前缀。
对于一个合法的$L$,必定存在一个划分方案$i,j$,满足$s_1[1…i] = s_2[j+1…L]$且$s_1[i+1…n] = s_2[1…j]$。而且,显然有$i \leq lcp_2(j+1), \, j \leq lcp_1(i+1)$
我们考虑枚举$j$。因为$L=i+j$,为了使得$L$尽可能大,需要$i$尽可能大。又因为上面的限制关系,此时相当于在$[1,lcp_2(j+1)]$内寻找满足$lcp_1(i+1) \leq j$的最大的$i$。
此问题可以用主席树解决,但是空间会炸。为了防止爆空间,可以对$j$按照$lcp_2(j+1)$排序,这样只需要线段树就能完成。
而$lcp$数组,则可以将$s_1,s_2$串起来求后缀数组解决。
时间复杂度$O(n \log n)$,期望得分50pt…
再讲讲正解。
首先$lcp$数组可以通过扩展KMP在$O(n)$内求出。接着,我们对$s_1$跑一次KMP,求出$s_1$的fail树。
对于一个合法的$L$,必定存在一个$i$,满足$s_1[1…i]=s_2[j+1…L]$且$L \leq i + lcp_1(i+1)$。同时,因为$s_1[1…i]=s_2[j+1…L]$,所以$j$只可能在对应节点的fail链上。
基于这点,只需要在fail树上维护$i+lcp_1(i+1)$的最大值即可判断$L$是否合法。
时间复杂度$O(n)$
CODE
CODE(50pt) - Click Here
CODE(100pt) - Click Here