CF809C - Click Here
Description
After a wonderful evening in the restaurant the time to go home came. Leha as a true gentlemen suggested Noora to give her a lift. Certainly the girl agreed with pleasure. Suddenly one problem appeared: Leha cannot find his car on a huge parking near the restaurant. So he decided to turn to the watchman for help.
Formally the parking can be represented as a matrix $10^9 \times 10^9$. There is exactly one car in every cell of the matrix. All cars have their own machine numbers represented as a positive integer. Let’s index the columns of the matrix by integers from $1$ to $10^9$ from left to right and the rows by integers from $1$ to $10^9$ from top to bottom. By coincidence it turned out, that for every cell $(x, y)$ the number of the car, which stands in this cell, is equal to the minimum positive integer, which can’t be found in the cells $(i, y)$ and $(x, j), 1 \leq i < x, 1 \leq j < y.$
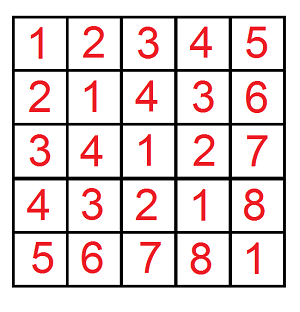
Leha wants to ask the watchman $q$ requests, which can help him to find his car. Every request is represented as five integers $x_1, y_1, x_2, y_2, k$. The watchman have to consider all cells $(x, y)$ of the matrix, such that $x_1 \leq x \leq x_2$ and $y_1 \leq y \leq y_2$, and if the number of the car in cell $(x, y)$ does not exceed $k$, increase the answer to the request by the number of the car in cell $(x, y)$. For each request Leha asks the watchman to tell him the resulting sum. Due to the fact that the sum can turn out to be quite large, hacker asks to calculate it modulo $10^9 + 7$.
However the requests seem to be impracticable for the watchman. Help the watchman to answer all Leha’s requests.
Input
The first line contains one integer $q$ ($1 \leq q \leq 10^4$) — the number of Leha’s requests.
The next $q$ lines contain five integers $x_1, y_1, x_2, y_2, k$
($1 \leq x_1 \leq x_2 \leq 10^9, 1 \leq y_1 \leq y_2 \leq 10^9, 1 \leq k \leq 2 \cdot 10^9$) — parameters of Leha’s requests.
Output
Print exactly $q$ lines — in the first line print the answer to the first request, in the second — the answer to the second request and so on.
Solutions
问题的关键在于表示出矩阵内的元素。
设题目所给出的矩阵为$A$。定义一个新矩阵$B$,满足$b_{x-1,y-1}+1=a_{x,y}$
则$b_{x,y}$可表示成$b_{x,y}=mex(S), S = \{ b_{i,y} \mid i < x \} \cup \{ b_{x,i} \mid i < y \}$
不难发现$b_{x,y}$与SG函数的定义相同。同时,会发现其后继状态的二元组只有一个元素改变,即该二元组为两个独立游戏的笛卡尔积。而对于每个独立游戏,其SG函数等价于Nim取石子,因此$b_{x,y}=x \, xor \, y$
现在回到本题上来,将$A$矩阵转换为$B$矩阵后,问题等价于询问$\sum_{x_1’ \leq x \leq x_2’} \sum_{y_1’ \leq y \leq y_2’} [x \, xor \, y \leq k’]x \, xor \, y$
对于这种区间问题,可以容斥,转换成询问$\sum_{x \leq x’} \sum_{y \leq y’} [x \, xor \, y \leq k’]x \, xor \, y$
考虑数位DP来解决。设$f[i][0/1][0/1][0/1],g[i][0/1][0/1][0/1]$表示到达第$i$位,是否抵达$x,y,k$的上界的方案数和答案和。
转移显然,此处略。
时间复杂度$O(q \cdot 2^5len)$
CODE
CODE - Click Here