HDU3896 - Click Here
Description
TC (Tian Chao) is magical place, as you all know…
The railways and the rail-stations in TC are fragile and always meet with different kinds of problems. In order to reach the destination safely on time, you are asked to develop a system which has two types of main functions as below.
1: A B C D, reporting whether we can get from station A to station B without passing the railway that connects station C and station D.
2: A B C, reporting whether we can get from station A to station B without passing station C.
Please notice that the railways are UNDIRECTED.
Input
For each test case, the first line will contain two integers N (2<=N<=100000) and M (1<=M<=500000), namely the number of stations and railways in TC.
Then each of the next M lines will have two integers, describing the two stations that a certain railway is connecting. After this, there comes a line containing a single integer Q (Q<=300000), which means the number of queries to make on the system.
The next Q lines will be queries. Each query begins with a integer, indicating the type of query, followed by 4 (the first type) or 3 (the second type) integers describing the details of the query as what mentioned above.
The stations are always labeled from 1 to N.
Output
For each test case, print “yes” or “no” in separated lines for the queries.
Solutions
这题是好题啊。。。刚开始还以为直接判断割顶和桥就好了,结果被KsCla无情的驳回了。。。
题目要求,删除某边或某点后是否依旧能够到达,这与联通分量极为相似。因此,我们可以利用联通分量的做法,遍历一次图,得到一棵DFS树。每个节点记录dfn,low,dep值,分别对应该点dfs序,该点能到达的最小dfs序以及该点所处深度。
对于删边询问,有几种情况。
此处不妨假设$dep[c]<dep[d]$,即d为c的儿子。
定义边集$E$为参与DFS树构建的边的集合。
1.若$(c,d) \notin E$,即$|dep[c]-dep[d]|>1$。那么显然删除这条边后,对这棵树中任意节点均无影响。(yes)
2.若$(c,d) \in E$且a,b同在d的子树内。显然a,b之间一定存在着a->d->b这样的路径,因此删边后不会有影响。(yes)
3.若$(c,d) \in E$且a,b同不在d的子树内。显然a,b之间的路径一定不会经过(c,d),因此删边后不会产生影响。(yes)
4.若$(c,d) \in E$且a,b有一个在d的子树内(此处不妨假设为a)。那么若要使得删边后不会产生影响,必定满足下列中的其中一种情况。
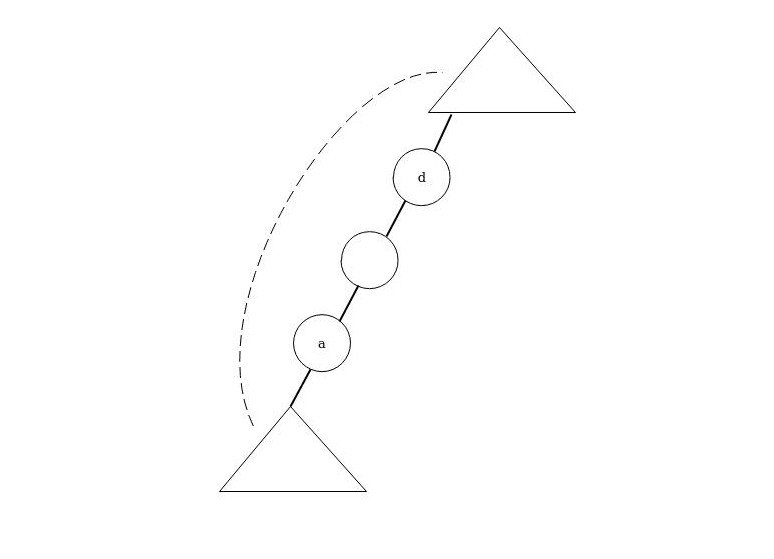
State1.这种情况下,a到达某个儿子节点,再从某条$(u,v) \notin E$的边到达b。此时,满足$low[a]<dfn[d]$,即a能够到达的节点是d的祖先。因此这种情况下,删边后不会产生影响。(yes)
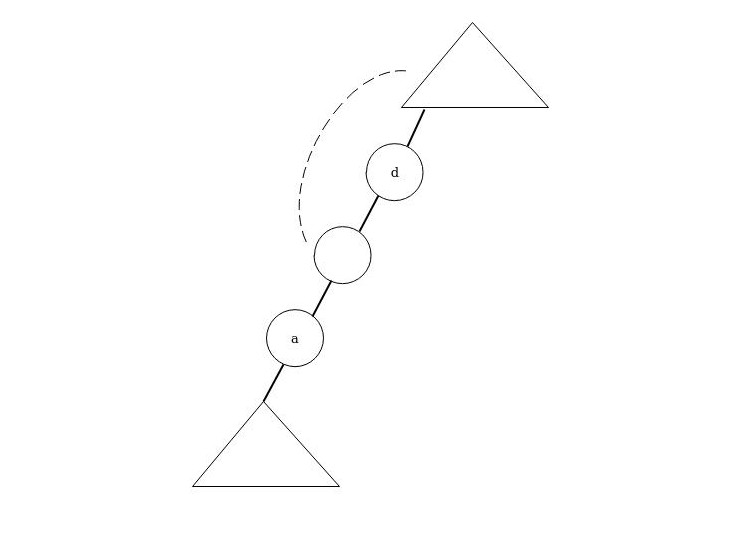
State2.这种情况下,a到达某个祖先节点f(同时为d的儿子节点),再从某条$(u,v) \notin E$的边到达b。此时,满足$low[f]<dfn[d]$,即f能够到达的节点是d的祖先。因此这种情况下,删边后不会产生影响。(yes)
由于我们不清楚,$(u,v) \notin E$的边是与a的儿子相连还是与a的祖先相连。为了能够一次判断出来,我们选择能够囊括所有满足要求的节点的信息进行判断,即a->d路径上的倒数第二个节点,假设为p。若$low[p]<dfn[d]$,删边不产生影响(yes),否则删边产生影响(no)。
理清了删边的情况后,删点就十分相似了。同样分为几种情况考虑。
1.若a,b同不在c的子树内。显然a,b之间的路径一定不会经过c,因此删点后不会产生影响。(yes)
2.若a,b有一个在c的子树内(此处不妨假设为a)。利用与删边时相同的技巧,选取a->c路径上的倒数第二个节点,假设为p。若$low[p]<dfn[c]$,删点不产生影响(yes),否则删点产生影响(no)。
3.若a,b同在c的子树内。
State1.若$LCA(a,b) \neq c$。显然$LCA(a,b)$也必定在c的子树内,因此存在a->$LCA(a,b)$->b这样的路径。删点后不会产生影响。(yes)
State2.若$LCA(a,b) = c$。若a要能够到达b,必须a能够到达c的祖先,b也能够到达c的祖先。利用删边时使用的技巧,选取a->c路径上的倒数第二个节点,假设为p;选取b->c路径上的倒数第二个节点,假设为q。若$low[p]<dfn[c] \& low[q]<dfn[c]$,删点不产生影响(yes),否则删点产生影响(no)。
P.S. 判断a是否在b的子树内的方法。
如果$LCA(a,b)=b$,则a在b的子树内;否则不在子树内。
或者可以记录每个节点开始dfs和结束dfs的时间戳,判断是否为包含关系,即可得知是否在子树内。
CODE
CODE - Click Here