UVALive3276 - Click Here
Description
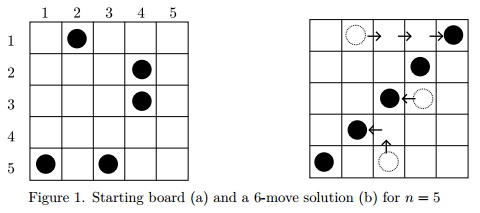
Hua and Shen have invented a simple solitaire board game that they call “The Great Wall Game.” The game is played with n stones on an n × n grid. The stones are placed at random in the squares of the grid, at most one stone per square. In a single move, any single stone can move into an unoccupied location one unit horizontally or vertically in the grid. The goal of the puzzle is to create a “wall,” i.e., to line up all n stones in a straight line either horizontally, vertically, or diagonally using the fewest number of moves. An example for the case n = 5 is shown in Figure 1(a). In Figure 1(b) it is shown that with six moves we can line all the stones up diagonally. No smaller number of moves suffices to create a line of five stones. (However, there are other solutions using six moves, e.g., we can line up all five stones in the third column using six moves.)
There is just one problem – Hua and Shen have no idea what the minimum number of moves is for any given starting board. They would like you to write a program that can take any starting configuration and determine the fewest number of moves needed to create a wall.
Input
The input consists of multiple cases. Each case begins with a line containing an integer n, 1<= n<=15. The next line contains the row and column numbers of the first stone, followed by the row and column numbers of the second stone, and so on. Rows and columns are numbered as in the above diagram. The input data for the last case will be followed by a line containing a single zero.
Output
For each input case, display the case number (1, 2, . . .) followed by the minimum number of moves needed to line up the n stones into a straight-line wall. Follow the format shown in the sample output.
Solutions
首先n十分小。因此可以枚举行、列和对角线,并求出每种情况的最优解。现在的问题是如何求最优解。
以行为例子,每一个棋子移动到该行的某个位置的代价为两点间的曼哈顿距离。而且,每个格子只能放一个棋子,每个棋子只能占用一个格子。很容易联想到二分图匹配。
构筑二分图$G=(V,E)$。每个节点$v$对应着一个棋子或格子,每条边$(u,v)$对应棋子u移动到格子v的代价(即u与v曼哈顿距离),最优解显然为该图的最佳完美匹配。
而所有最优解的最小值,即为该题目的答案。
此处还有要注意的一点是,一个匹配方案必定对应着一个合法的移动方案。换言之,通过合理的顺序,可以使得任意棋子的移动不受到其他棋子的影响。
CODE
CODE - Click Here