BZOJ3884 - Click Here
Description
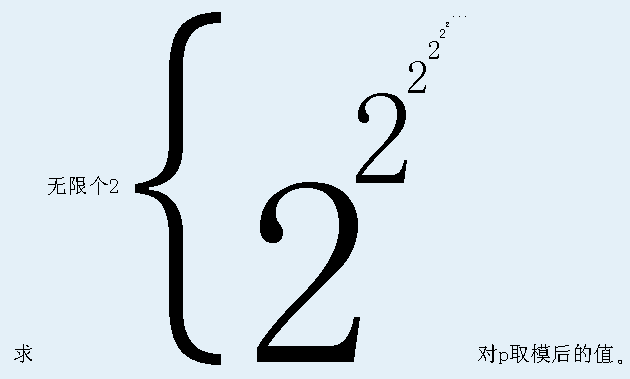
Input
第一行给出一个正整数T。
接下来T行,每行一个正整数p,代表你需要取模的值。
对于100%的数据,T<=1000,p<=10^7
Output
T行,每行一个正整数,为答案对p取模后的值。
Solutions
给出题人(PoPoQQQ)跪了。感觉这种无限的题目都要靠减小模数来解决啊?(雾)
令$p=2^k \times q$,其中$q$为奇数(分解必定唯一)。
则$2^{2^{2^{2…}}}mod\ p=2^k \times (2^{2^{2^{2…}} - k}\ mod\ q)$。
由于$q$为奇数,因此$q$与$2^{2^{2^{2…}} - k}$互质。
所以由欧拉定理得$2^k \times (2^{2^{2^{2…}} - k} \, mod \, q)=2^k \times (2^{(2^{2^{2…}} - k) \, mod \, \phi(q)} \, mod \, q)$。
减法可以化开,然后又变成了原来的格式。但是模数变小了,模数变小了,模数变小了!!!
也就是说,这样子不断的化下去,最后模数会变成1,此时答案是确定的。(任何数mod 1均为0)
因此这样子不断递归下去就可以得到最终解。
再考虑一下时间复杂度,因为每次模数至少会除以2,因此最多$log \, q$次模数就会变成1,再加上预处理出欧拉函数的时间为$O(q)$,所以总时间为$O(q+Tlog\ q)$
CODE
CODE - Click Here